두 힘의 합성법 (삼각함수 응용)
안녕하세요. 쏘쏘입니다.
이번 포스팅에서는 힘의 합성에 대해 알아보겠습니다.
힘의 합성 중에서도 각기 다른 방향인 두 힘의 합성에 대해 설명드리겠습니다.
먼저 임의의 방향으로 작용하는 힘 F1, F2를 그려보겠습니다.
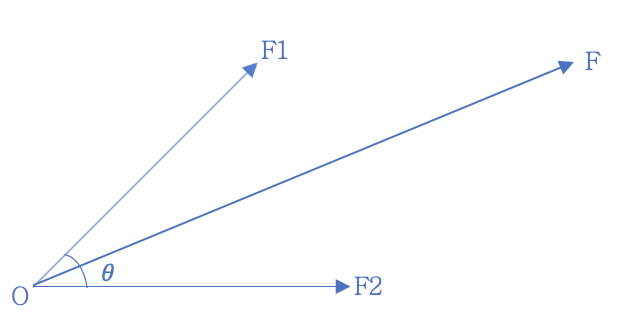
힘 F1과 F2가 이루는 각을 𝜃, F1과 F2를 합성한 힘을 F로 표기하였습니다
이제 여기서 sin, cos 삼각함수를 이용하여 F값을 구할 수 있습니다.
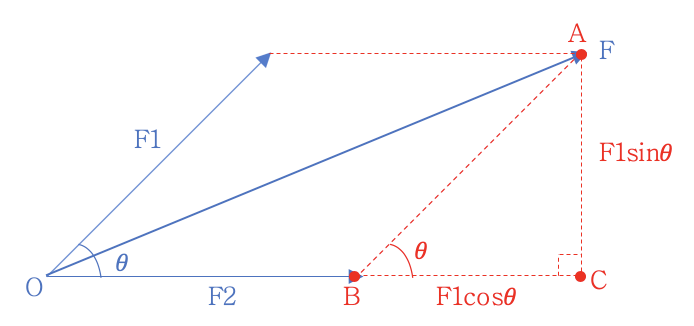
가상의 선을 그어서 평행사변형을 만들고 A, B, C 꼭짓점을 찍었습니다.
A-O-C가 이루는 삼각형은 직각 삼각형이며,
빗변 OA의 값이 F1, F2 두 힘을 합성한 힘 F입니다.
그리고 A-B-C도 직각 삼각형을 이루고 있으며,
AB와 BC가 이루는 각 𝜃는 F1과 F2가 이루는 각 𝜃와 동일합니다.
또한 평행사변형이므로 AB는 힘 F1과 동일합니다.
이제 AC와 BC의 값을 구해보면 아래와 같습니다.
sin𝜃=AC/AB=AC/F1 따라서 AC=F1*sin𝜃
cos𝜃=BC/AB=BC/F1 따라서 BC=F1*cos𝜃
그리고 자연스레 OC의 값은 F1*cos𝜃+F2가 됩니다.
이제 삼각형 AOB에서 피타고라스의 정리에 의해 빗변 OA를 구할 수 있으며,
이 값이 F1과 F2 힘의 합성값입니다.

이렇게 두 힘의 합성이 구해졌습니다.
다음 포스팅에서는 세 힘의 평형, 라미의 정리에 대해서 이해하기 쉽도록 설명드리겠습니다.
글 읽어 주셔서 감사합니다.
- by 쏘쏘 -
2020/01/25 - [소소한 공부방/기초 수학] - [삼각함수 기초 #1] cosθ, sinθ, tanθ 란 ???
[삼각함수 기초 #1] cosθ, sinθ, tanθ 란 ???
안녕하세요. 쏘쏘입니다. 삼각함수 기초에 대하여 설명드리겠습니다. 삼각함수를 간단히 말하자면 삼각형의 각 변의 길이와 각도가 연관된 함수입니다. 삼각함수의 기본을 알고 계시면 나중에 어려운 문제가 나오..
ssossoblog.tistory.com
2020/01/27 - [소소한 공부방/기초 수학] - [삼각함수 기초 #2] cosθ, sinθ, tanθ의 역수 secθ, cosecθ, cotθ에 대하여
[삼각함수 기초 #2] cosθ, sinθ, tanθ의 역수 secθ, cosecθ, cotθ에 대하여
안녕하세요. 쏘쏘입니다. 사람들은 코사인, 사인, 탄젠트뿐만 아니라, 아크코사인, 하이퍼사인, 코탄젠트 등등 삼각형을 가지고 여러 가지를 만들어 놓았습니다. 이번 시간에는 기본 삼각함수 cos, sin, tan의 역..
ssossoblog.tistory.com
2020/01/29 - [소소한 공부방/기초 수학] - [삼각함수 기초 #3] sinθ, cosθ, tanθ 기본적인 값 구하기 (30˚, 45˚, 60˚)
[삼각함수 기초 #3] sinθ, cosθ, tanθ 기본적인 값 구하기 (30˚, 45˚, 60˚)
안녕하세요. 쏘쏘입니다. 교과 과정에서 cos/sin/tan의 의미를 배우게 되면 기본 각도들에 대한 값을 먼저 배울 겁니다. 대학에서는 cos30˚, 45˚, 60˚ 의 값에 대해서도 굳이 외우지 않아도 됩니다. 공학용 계..
ssossoblog.tistory.com
2020/02/03 - [소소한 공부방/기초 수학] - [삼각함수 기초 #4] cos0˚, sin0˚, tan0˚ / cos90˚, sin90˚, tan90˚ 값 구하기
[삼각함수 기초 #4] cos0˚, sin0˚, tan0˚ / cos90˚, sin90˚, tan90˚ 값 구하기
안녕하세요. 쏘쏘입니다. 이번 시간에는 cos, sin, tan의 0˚와 90˚ 값에 대해 설명드리겠습니다. 먼저 x, y 좌표계에 삼각형과 원을 그려보겠습니다. 위의 그림에서 cosθ=x/r, sinθ=y/r, tan&theta..
ssossoblog.tistory.com
'소소한 공부방 > 기초 물리와 역학' 카테고리의 다른 글
| 물체의 운동 주요 그래프 (미분, 적분 응용) (0) | 2020.03.04 |
|---|---|
| 응력의 종류 (인장, 압축, 전단) (0) | 2020.03.03 |
| 등가속도 운동 3가지 관계식 구하기 (0) | 2020.02.25 |
| [모멘트 #3] 모멘트의 부호 규약 (+ / - 부호) #2 (2) | 2020.02.17 |
| 하중의 종류 (0) | 2020.02.02 |