[삼각함수 기초 #3] sinθ, cosθ, tanθ 기본적인 값 구하기 (30˚, 45˚, 60˚)
안녕하세요. 쏘쏘입니다.
교과 과정에서 cos/sin/tan의 의미를 배우게 되면 기본 각도들에 대한 값을 먼저 배울 겁니다.
대학에서는 cos30˚, 45˚, 60˚ 의 값에 대해서도 굳이 외우지 않아도 됩니다. 공학용 계산기를 사용해서 풀거든요.
왜냐면 대학에서는 위의 기본 각도 외에 수많은 각도에 대해서 계산을 해야 하는데 31˚는 얼마, 42˚는 얼마인지 모두 다 외울 수가 없거든요.
중학교, 고등학교에서는 기본 각도에 대한 값은 알고 있어야 할 겁니다. 아주 오래전이지만 저의 학창 시절에 시험에도 나오고 했던 기억이 있거든요. 그래서 이번 시간에는 cos60˚= 1/2, tan60˚=√3 등 기본적인 각도에 대한 값들에 대해 쉽게 이해할 수 있게 알려 드리겠습니다.
우선 삼각형을 그려보겠습니다.
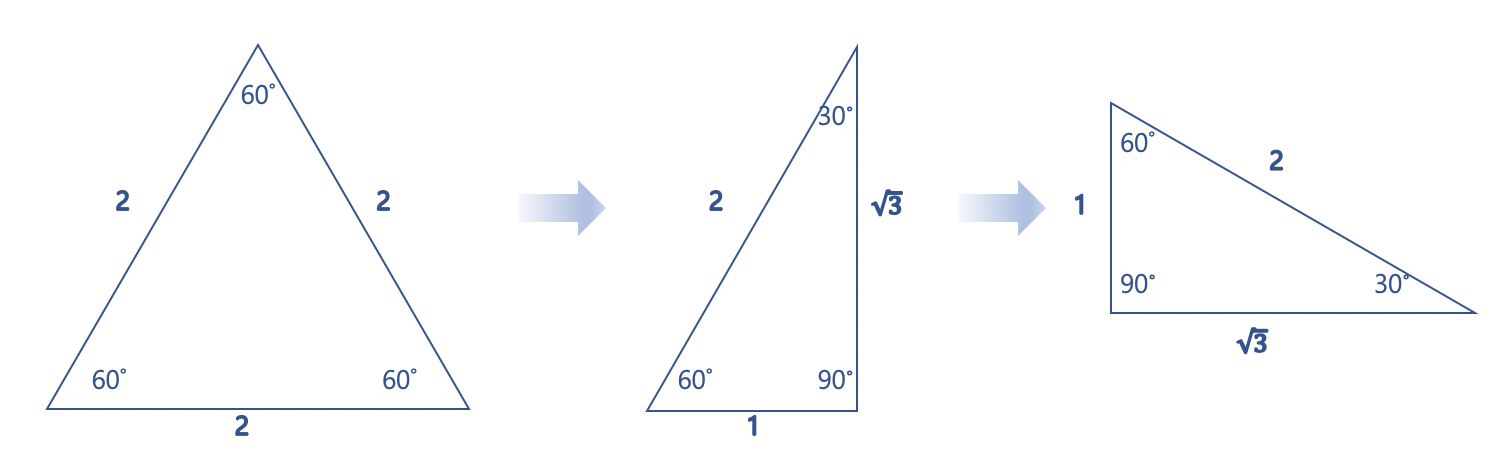
먼저 왼쪽과 같이 각 변의 길이가 2인 정삼각형을 그리고 가운데 그림과 같이 삼각형을 반으로 나누었습니다. (변의 길이가 1인 정삼각형이 아니라 길이가 2인 삼각형을 그린 이유는, 개인적인 생각이지만 변의 길이가 1일 때보다 이해하기 더 쉬워서입니다.)
정삼각형을 반으로 나누었으니까 밑변의 길이는 1이 되고, 빗변의 길이는 그대로 2입니다.
그렇다면 높이는 어떻게 구할까요? 피타고라스의 정리 빗변²=밑변²+ 높이²를 활용하면 높이가 √3 이 되는 걸 알 수 있습니다.
이렇게 반으로 나눈 삼각형에서 cos, sin, tan의 30˚, 60˚ 값을 구할 수 있습니다.
먼저 가운데 삼각형을 기준으로 cos60˚, sin60˚, tan60˚를 구하면,
→ cos60˚=1/2, sin60˚=√3/2, tan60˚=√3이 됩니다.
그리고 오른쪽 그림처럼 길이 √3인 변을 밑변으로 생각하고 삼각형을 돌려봅시다. 그러면 높이 1이고 빗변이 2가되지요.
이제 이 상태에서 cos30˚, sin30˚, tan30˚을 구하면,
→ cos30˚=√3/2, sin30˚=1/2, tan30˚=1/√3이 됩니다.
이제 cos45˚, sin45˚, tan45˚에 대한 삼각형을 그려봅시다.
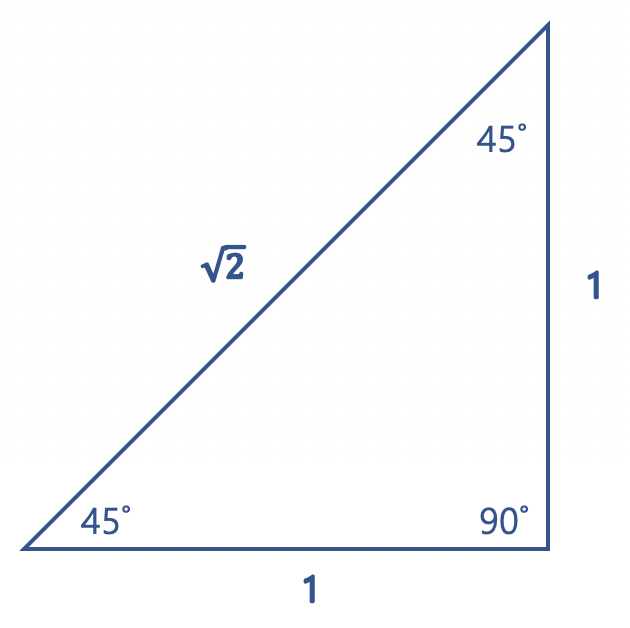
밑변과 높이가 1인 삼각형을 그립니다. 그렇게 되면 빗변은 자연스레 √2가 됩니다.
그럼 여기서 cos45˚=1/√2, sin45˚=1/√2, tan45˚=1 임을 알 수 있습니다.
이번에 다루지 않은 0˚, 90˚, 180˚ 등에 대해서도 추가로 포스팅하겠습니다.
도움이 되셨기를 바라며, 다른 주제로 다시 찾아뵙겠습니다.
- by 쏘쏘 -
[관련 글] - [삼각함수 기초 #1] cosθ, sinθ, tanθ 란 ???
[삼각함수 기초 #1] cosθ, sinθ, tanθ 란 ???
안녕하세요. 쏘쏘입니다. 삼각함수 기초에 대하여 설명드리겠습니다. 삼각함수를 간단히 말하자면 삼각형의 각 변의 길이와 각도가 연관된 함수입니다. 삼각함수의 기본을 알고 계시면 나중에 어려운 문제가 나오..
ssossoblog.tistory.com
[관련 글] - [삼각함수 기초 #2] cosθ, sinθ, tanθ의 역수 secθ, cosecθ, cotθ에 대하여
[삼각함수 기초 #2] cosθ, sinθ, tanθ의 역수 secθ, cosecθ, cotθ에 대하여
안녕하세요. 쏘쏘입니다. 사람들은 코사인, 사인, 탄젠트뿐만 아니라, 아크코사인, 하이퍼사인, 코탄젠트 등등 삼각형을 가지고 여러 가지를 만들어 놓았습니다. 이번 시간에는 기본 삼각함수 cos, sin, tan의 역..
ssossoblog.tistory.com
[관련 글] - [삼각함수 기초 #4] cos0˚, sin0˚, tan0˚ / cos90˚, sin90˚, tan90˚ 값 구하기
[삼각함수 기초 #4] cos0˚, sin0˚, tan0˚ / cos90˚, sin90˚, tan90˚ 값 구하기
안녕하세요. 쏘쏘입니다. 이번 시간에는 cos, sin, tan의 0˚와 90˚ 값에 대해 설명드리겠습니다. 먼저 x, y 좌표계에 삼각형과 원을 그려보겠습니다. 위의 그림에서 cosθ=x/r, sinθ=y/r, tan&theta..
ssossoblog.tistory.com
[관련 글] - [삼각함수 기초 #5] 삼각함수 각도 변환 cos(90˚-θ), sin(90˚-θ), tan(90˚-θ) 값 구하기
[삼각함수 기초 #5] 삼각함수 각도 변환 cos(90˚-θ), sin(90˚-θ), tan(90˚-θ) 값 구하기
안녕하세요. 쏘쏘입니다. 이번 포스팅에서는 오랜만에 삼각함수 기초 내용을 다루어 볼게요. 4번의 포스팅까지 cos, sin, tan의 0˚와 90˚ 값을 구하는 것까지 설명드렸었는데, 이번부터는 각도 변환에 대해서 설..
ssossoblog.tistory.com
'소소한 공부방 > 기초 수학' 카테고리의 다른 글
| [미분 #1] 미분의 개념과 필요성 (0) | 2020.02.21 |
|---|---|
| 함수의 의미와 종류 (0) | 2020.02.04 |
| [삼각함수 기초 #4] cos0˚, sin0˚, tan0˚ / cos90˚, sin90˚, tan90˚ 값 구하기 (0) | 2020.02.03 |
| [삼각함수 기초 #2] cosθ, sinθ, tanθ의 역수 secθ, cosecθ, cotθ에 대하여 (1) | 2020.01.27 |
| [삼각함수 기초 #1] cosθ, sinθ, tanθ 란 ??? (0) | 2020.01.25 |